Table of Contents
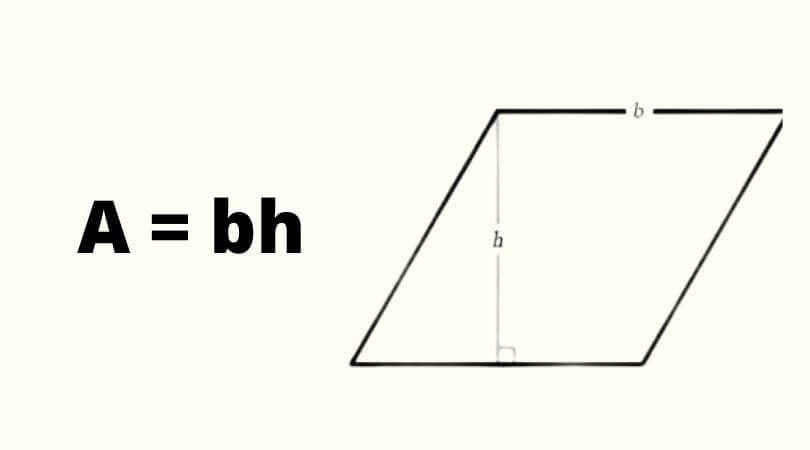
In mathematics, it is very difficult to consider an area of any specific figure. Today, we will discuss the area of Parallelogram for the students. To calculate the area of the Parallelogram, it is important to know the space occupied by the given Parallelogram. The formula given for it is b * h where b refers to the base and h refers to the height of the Parallelogram. The answer will come in the square units. For example, if 6 cm is multiplied by 3 cm, the answer will be equal to 18 cm square units. Today, we will discuss some important factors about Parallelogram.
What is Parallelogram and Its Types?
Usually, you can find out numerous geometrical shapes in mathematics like rectangle, square, rhombus, trapezium, and others. In the same manner, Parallelogram is a kind of geometrical shape that looks like a quadrilateral. Reality in, a Parallelogram has four sides in which opposite sides are equal to each other. In this regard, you should know about some examples for it. If a Parallelogram is “EFGH”, then EF is equal to the GH. On the other hand, EG will be equal to the FH. However, Parallelogram is also classified in several names like square, rhombus, and rectangle. All of these poses have different properties from each other. In the next paragraph, we will know some important properties of Parallelogram along with their types.
Properties of Parallelogram
As we mentioned above, Parallelogram is a kind of quadrilateral that has parallel and opposite sides equal. Now, we discover the several properties of Parallelogram easily. Here are some properties that you should know about it:
- The opposites sides of the Parallelogram will always be parallel and equal.
- Each angle of the Parallelogram opposite to each other will equal. However, a diagonal can bisect a Parallelogram into two triangles. Both the triangles will congruent to each other.
- Generally, Parallelogram is subdivided into three types. These are, for example, squares, rhombus, and rectangles. Each shape has its properties according to the basis of nature.
- In every shape, one thing is common the diagonal of all of them bisects themselves accordingly.
Kinds of Parallelogram: Rhombus, Square, and Rectangle
Here are the types of Parallelogram:
- A square is a kind of Parallelogram that has four equal and parallel sides. In this type of Parallelogram, the angle of each side measures about 90 degrees.
- A kind of Parallelogram is a two-dimensional structure. It mainly consists of 4 corners and sides.
- This is an extraordinary shape of a Parallelogram. In such a type of Parallelogram, you will always find two pairs of parallel sides. This is called Rhombus.
Some Examples Based on the Area of Parallelogram
As we discussed above that the mathematical formula of Parallelogram is defined as “b*h”. In this formula, be denoted as base or h denoted as the height of Parallelogram. Let’s know some examples to clarify this topic easily:
Example 1: Calculate the area of a Parallelogram, if the height and base of 4 cm and 5 cm respectively?
As per the question,
Base of the Parallelogram = 4 cm
Height of the Parallelogram = 5 cm
By using the formula of area of Parallelogram = b*h
4 cm * 5 cm – 20 cm square units.
Hence, the area of the Parallelogram of the given base and height is equal to 20 cm square units.
Example 2: Define the area of a Parallelogram, if the height and base are 10 cm and 7 cm respectively?
As per the question,
Base of the Parallelogram = 10 cm
Height of the Parallelogram = 7 cm
According to the formula of area of Parallelogram = b*h
10 cm * 7 cm = 70 cm square units.
Hence, the area of the Parallelogram for the given height and base of equal to the 70 cm square units.
If you want to know more details about the area of Parallelogram, you should visit the Cuemath and book a free session. Here, you will get all the details about the Parallelogram.
Also Read :- What is the use of QR codes in Daily Communication with Science?



